

(Scroll to the bottom of comment to see a picture of what I'm talking about) We have the same number of different possibilities as before, so we keep the denominator the same. Heads could be first, second, third, fourth, fifth, sixth, seventh, eighth, ninth, or tenth, so that's ten different ways you would have just one heads. If you want only one heads out of ten, there are going to be ten different ways to get one head. In order to find P(One Heads) you're going to have to think. P(No heads) is simple enough to find, just take the probability of tails to the tenth power. Since there are ten repetitions of the experiment, and two possible outcomes per experiment, the number of different outcomes is 2 ^ 10, or 1024. P(at least 2 heads) = 1 - P(No heads) - P(One heads) However, instead of just subtracting "no tails" from one, you would also subtract "one heads" from it too. You would use a similar method, which involves what we've been doing. Learn more about the coins featured in the Coin Flip game in the gallery below.Short Answer: You are right, we would not use the same method. The more you flip a coin, the closer you will be towards landing on heads 50% – or half – of the time. This represents the concept of relative frequency. When a coin is flipped 1,000 times, it landed on heads 543 times out of 1,000 or 54.3% of the time. When a coin is flipped 100 times, it landed on heads 57 times out of 100, or 57% of the time. When a coin is flipped 10 times, it landed on heads 6 times out of 10, or 60% of the time. It turns out that the more you do something, like toss a coin, the higher chance you have of reaching the expected probability, which, in this case, is 50%. Is the number closer to 50%? Most likely, it is. If you test this with our Coin Flip game, you’ll see that is not always the case. Statisticsīased on the calculations we just did, you expect that if you toss a coin 10 times, it will land on heads 50% of the time. So, the probability of landing on heads is (1/2) x 100, which is 50%. (Desired outcome(s) / # of possible outcomes) x 100 Percentage means ‘out of 100,’ and it can be expressed as: This means that the probability of landing on heads is 1/2. A coin has 2 possible outcomes because it only has two sides (heads or tails). Because you only pick one outcome – let’s say, heads – the desired outcome is 1. When you flip a coin, you choose your desired outcome – the side you want it to land on (either heads or tails). As a fraction, it is represented as:ĭesired outcome(s) /# of possible outcomes
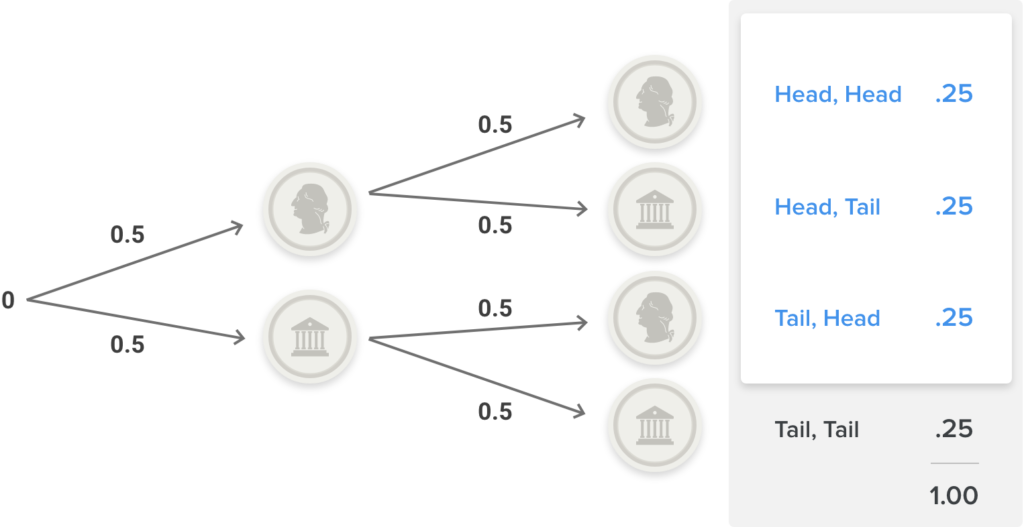
Probability can be represented as a fraction or a percentage. Probability measures the likelihood that an event will occur, such as how likely a coin will land on heads when you flip it. Learn more about the mathematical origins of flipping a coin below. They are also used to teach statistical concepts, including probability and relative frequency. Probability and StatisticsĬoin flips are often used to learn about basic mathematical concepts, including fractions and percentages. Today, a coin toss is used in some sporting events to determine which team will possess the ball.
The city of Portland, Oregon is rumored to be named as such due to the flip of a coin. In 1903, Orville and Wilbur Wright tossed a coin to decide who would fly first in their historic flight in Kill Devil Hills, North Carolina.

In more recent years, it has been linked to probability and statistics. The coin flip dates back to the Roman Empire, where it was originally known as “Heads or Ships”. Mint’s Coin Flip game? Learn more about the history of coin flips, the mathematical origins of coin flips, and history behind the coins featured in the game.


 0 kommentar(er)
0 kommentar(er)
